Standard deviation measures how much variation there is within a group of things. For example, if we randomly select a group of 5 people and measure their height, almost certainly not every height will be the same; there will be some variation in height. But how much? How do we measure how variable something is? Standard deviation is one such measure.

Suppose we measure the height of 5 random people (we'll say in centimeters) and we record the following:

177, 170, 173, 168, 178.

As the reader can surely see, there is some variation here. But now suppose we measure the height of 5 more people and record the following:

140, 185, 172, 191, 99.

Clearly, there is more variation in this second group than in the first. But how much variation? How do we quantify it?

Let us answer this question by first turning our focus to writing. Word lengths vary. Sentence lengths vary. But how much do they vary? We shall first consider a simple example. Suppose we just sat down at our typewriter and wrote

I saw it. It was divine. I wanted it.

Notice that in this passage there is very little variation in the lengths of sentences. In fact, there is NO variation at all since all three sentences have only three words. The average sentence length in the above passage is (3+3+3)/3 = 3 words, and the "typical" deviation from this average is 0 words since every sentence length is the same.

But suppose we wrote:

Yes. I know you. I have seen your face.

The average sentence length is again (1+3+5)/3 = 3 words, but this time there is clearly some variation between the sentence lengths. But how much variation? The first sentence is 2 words below the average, the second sentence length is equal to the average, and the third sentence is 2 words above the average. Thus, the "deviations" from the average are -2, 0, and 2.

If we average these deviations we get (-2+0+2)/3=0. So we cannot simply take an average since the average of the deviations is always 0. So statisticians have a clever way of getting around this by taking a different kind of average: take an "average" of the squares of the deviations and then take a square root (in a sense to "undo" the squares). That is:


for an "average" of 2. So the "standard" deviation from the average of 3 words is 2 words.

The reader will notice that we divide by one less than the number of observations. This is done for statistical reasons and actually works better when we "average" the squared deviations.

Now consider the passage:

Wait. Haven't I seen you before? You're that fella who hit me in the eye on the subway yesterday. I'm gonna git you.

Here there is even more variation between sentence lengths. But how much more? Let's find out. The average sentence length is (1+5+13+4)/4 = 5.75 words, but this time the first sentence is 4.75 words below the average, the second is 0.75 below, the third is 7.25 words above, and the fourth is 1.75 words below, that is, our deviations from the average are -4.75, -0.75, 7.25, and -1.75. Then


So the "standard" deviation from the average is about 5.12 words. Thus, there is more deviation between sentence lengths in this example passage than the previous, just as we suspected. But now we can actually quantify that difference and say exactly how much more variation there is in the present passage as compared to the previous passage.

We shall compare two writing samples. The first being Oscar Wilde's "The Happy Prince," and the second the text of George Washington's 1796 State of the Union Address.

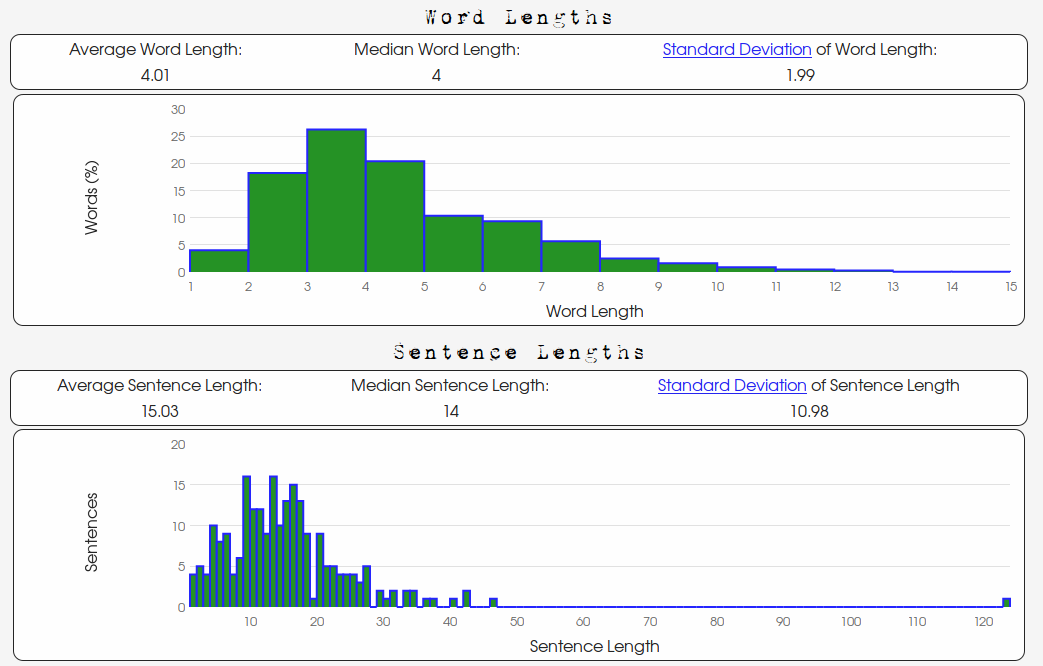
Below is both the word and sentence length distribution data for Oscar Wilde's "The Happy Prince":

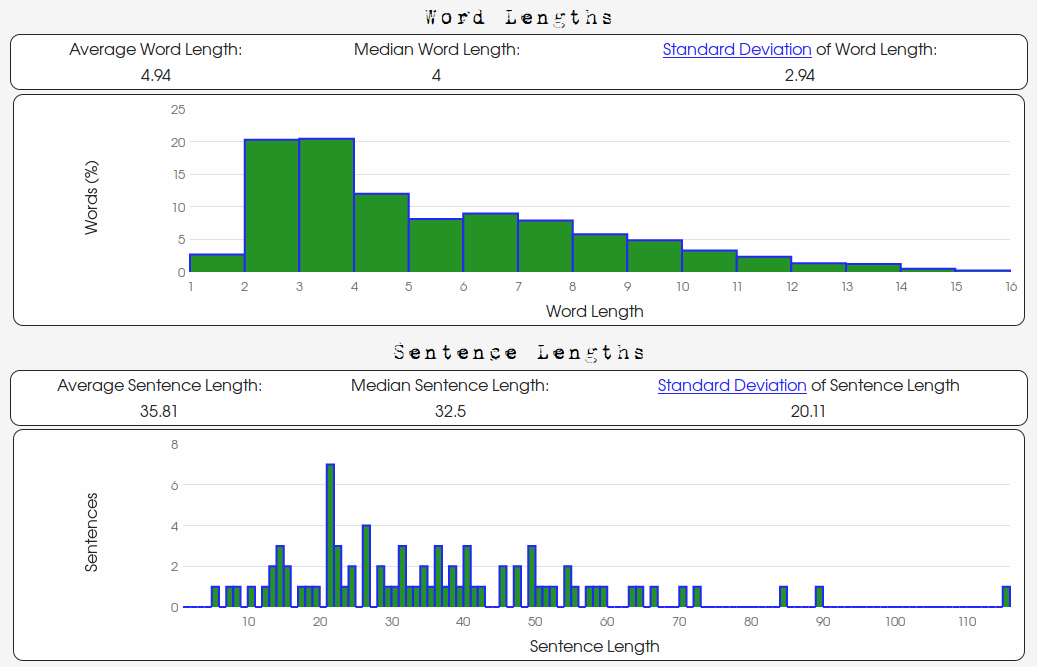
And the word and sentence length distribution data for George Washington's 1796 State of the Union Address:

There are clearly a differences between Oscar Wilde's story and George Washington's speech. The lengths of Wilde's sentences are less "spread out" than Washington's and their respective standard deviations of 10.98 words and 20.11 words are indicative of this.

The reader will also notice the differences in the word length data. The "shape" of the word length distribution of Wilde's text is markedly different than Washington's. Wilde's "trails off" or "falls off" more quickly. Also, the "center" of Washington's word length distribution is "more to the right" as indicated by a higher word-length average. We can see that Washington uses larger words more frequently and with more variety. There is more variation between word lengths. How much more? Well, 0.95 letters more than Wilde to be exact! Moreover, Washington's average word length is almost an entire letter more (which the experienced user of this site will tell you is quite a large difference). In summary, Washington's word lengths are longer on average (Washington's average: 4.94, Wilde's average: 4.01) and are more varied (Washington's standard deviation: 2.94, Wilde's standard deviation: 1.99).

If we consider the nature of both these texts, the above observations are not surprising. "The Happy Prince" is a story written for children, whereas, Washington's State of the Union is charting the course of a young nation. Typically, a public address seeks to avoid monotone in order to hold a listener's interest and will vary in intonation, rhythm, and likely sentence length. It also requires the command of a larger vocabulary. On the other hand, children's stories are typically is told in shorter sentences and words to facilitate better understanding of young readers and listeners. And if you read both texts (which are available on this website on the homepage), you will certainly catch the difference in tone and rhythm.

Among other quantifiable aspects of writing which are measured by this website, we offer standard deviations of both word and sentence lengths because (as we hope the above example has illustrated) they can give us information about how we write and who our audience is.